Rasch Model Origin

Next      Back     Start                            Chapter 9

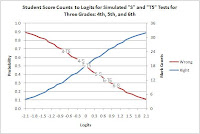
The Rasch model came into being in response to data that Dr. Georg Rasch graphed. He administered two tests to each student in several grades. The 6^th graders made fewer wrong marks than the 5^th and 4^th graders on the same questions. 

He plotted one test on the horizontal axis and the other on the vertical axis. He observed, “the three assemblies of points which illustrated the amount of errors in the different grades immediately succeeded each other and pointed towards the 0-point.”

Further, he noted that one error on one test (“S”) corresponded to 1.2 errors on the other test (“T5”). This ratio remained the same for each of the three grades, 4^th, 5^th, and 6^th. “An expression for the degree of difficulty of one test in relation to another has thus been found”.

For this constant ratio to happen, the chance to mark a right answer must be equally good whenever the ratio of student proficiency to question difficulty is the same. A student has a 50% chance of correctly marking items when student ability equals question difficulty. “The chances of solving an item thus come to depend only on the ratio between proficiency and degree of difficulty, and this turns out to be the crux of the matter.”

The average wrong score for each of the six tests is marked on the wrong answer ogive (curve). The 5^th grade “T5” simulated (5-T5) test had an average score of 50%. This 50% score is located at the zero (0) point on the logit scale. (Remember, an ogive is a normal distribution expressed in logits.)

Applying the Rasch model to the logit values, without further information, only returns the original right mark raw scores: A count of 27 out of 36 total questions is 27/36 or 75%, is odds of right/wrong or 75/25 or 3, and as logits is log(odds) or log(3) or 1.1. In reverse, percent is exp(logits)/(1+exp(logits)) or exp(1.1)/(1+exp(1.1)) or 3/(1+3) or 3/4 or 75%, and is 0.75 of 36 total or a count of 27. 

The missing information is obtained by replacing the values for marks, 1 and 0, for right and wrong, in a mark data matrix, as in PUP Table 3, with the probability of students making a right mark, that ranges from 0 to 1.

Winsteps fits mark data to the Rasch model, using probabilities, to produce estimated student ability and item difficulty measures on the same horizontal logit scale. It is from these estimated measures that the Rasch model creates (maps) predicted raw scores used as cut scores.

Next     Back     Start

Perfect Rasch Model

Next    Back    Start                         Chapter 8

Defining relationships creates mathematical models. The sum is the total of all the numbers added. The mean or average is the sum divided by the number of numbers added. The variation in the added numbers is the sum of the squares of the difference between each number and the mean. The mean square or variance is the sum of squares divided by the number of numbers added. The standard deviation (SD) for the mean is the square root of the mean square. These all assume the data fit the normal curve distribution. They are used by both PUP and Ministep.

The cumulative normal distribution (the s-shaped curve or [ogive]) sums the normal distribution. This changes the view of the data from counts by student scores to proportion or percent by student z-scores. 

Information Response Theory (IRT) is expressed in three models. 

The two-parameter IRT (2-P) model and the cumulative normal distribution almost match. The one-parameter IRT (1-P) model drops out a constant (1.7) needed to make the above match. This gives the 1-P and Rasch model ogives a fixed slope. The three-parameter IRT (3-P) includes guessing. The lower asymptote descends to the test designed guessing value (0.25 for 4-option questions) rather than to zero.

The Rasch model is the easiest model to use with the least requirements. It only requires student scores and item difficulties. It omits discrimination (or slope in 2- and 3-P models) by only using data that fit the perfect Rasch model requirements.

The Rasch model also omits any adjustment for guessing on multiple-choice tests. “Critics of the Rasch model claim this to be a fatal weakness.” (p64, Bond and Fox, 2007). This depends upon how the Rasch model is used. If the area of action is far enough from the lower asymptote, guessing can be of little effect (average score of 75% and cut score of 60%, for example). [Winsteps can clip the lower asymptote.

The all-positive normal scale (0 to 100%) is replaced with a logit scale (-4 to +4). All the ogives, except for the 3-P IRT, cross a point defined as zero logit and 0.5 probability. Student ability and question difficulty are both plotted on the logit scale. A student is expected to mark a right answer 50% of the time when ability and difficulty match. A student with an ability one logit higher than a question with zero logit difficulty is expected to make a right mark 73% of the time.

Item ogives are called item characteristic curves (ICC). A test ogive is called a test characteristic curve (TCC). A TCC is created by combining ICCs. Expected raw scores for setting test cut-scores are obtained by mapping with a TCC from the logit scale.

Next     Back    Start 

Standard Units

Next   Back   Start                        Chapter 7

Education has a number of standard units. One is basic to assigning probabilities to events like right marks on a test: the standard deviation.

Random error creates the normal distribution (the normal or bell curve). The distribution happens every time, with a large enough sample. Random error gives each individual an honest and fair chance within the distribution.

The point on the side of the normal curve where it changes bending from up to down, or down to up, is one standard deviation (SD). Some 95% of a sample is expected to fall within +/- 2 SD of the mean. When observed results do not fit within +/- 2 SD (the 5% level of significance) we know to look for a cause, other than chance.

Raw test scores are standardized, turned into Z scores, by dividing them by their SD. Two class distributions can be equated by matching the Z scores or by shifting and stretching one of the distributions to fit the other one. The idea is that students who have similar Z scores should have similar grades. The conversion can be made from Test A to Test B or from Test B to Text A.

Z scores permit adjusting two sets of raw test scores along one dimension. The Rasch model makes adjustments in two dimensions at the same time, raw scores and item difficulty. The Rasch model uses a t-statistic to detect unacceptable fit.

The t Outfit Zstd Outfit Zstd on the Winsteps bubble chart is a standardized indicator of how well student and item performances fit the Rasch model's requirements.

Positive values reflect underfit to the Rasch model or unfinished on PUP Table 3a. Negative values reflect overfit to the Rasch model or highly discriminating on PUP Table 3a. A student or item performance does not fit if the difference is more than two t-statistic units away from the perfect model. Or, for example, the performance of Item 21, 2.3 t Outfit Zstd exceeds two t-statistic units, may still be do to chance one out of 20 times (the 5% [level of significance).

Next    Back   Start

Winsteps Person & Item Bubble Chart

Next    Back    Start                        Chapter 6

Ministep prints out a bubble chart relating how well the estimated measures for persons (blue) and items (red) fit the Rasch model.

A comparison of the two methods for expressing item discrimination (Rasch fitness and PUP item discrimination) reveals an interesting similarity: The two distributions are related. Four of the more difficult items (4, 10, 19, and 21) on the bubble chart show an almost perfect match, on the scatter chart, between fitness and item discrimination.

The Rasch overfit item 4 falls in the PUP distribution at high discrimination (upper left). The Rasch underfit item 21 falls in the PUP distribution at low discrimination (lower right). Fitness and item discrimination are negatively related. The standard fit statistic, outfit,  from Tables 17.1, Person in Measure Order (blue), and 13.1, Item in Measure Order (red) are used in these two charts.

The Rasch model requires uniform discrimination (which is why the model can ignore discrimination after discarding overfit and underfit persons and items, that is, performances that show too high and too low discrimination). Values below -2 are excessive overfit and above +2 are excessive underfit. The person and item performances on this test fit the Rasch model requirements with the exception of item 21. More high scoring students marked it wrong than low scoring students.

The Rasch bubble chart presents results in terms of estimated measures of student ability and item difficulty. The two students (blue) with scores of 100% (high ability) fall at the top of the chart. The three items (red) marked correctly by all students fall at the bottom of the chart (low difficulty).

The three low scoring students (blue 16, 18, and 21) are expected to have less ability (lower on the bubble chart) than needed to answer the two items (red 10 and 19), with an estimated difficulty measure higher (higher on the bubble chart) than their estimated student ability measures.

The bubble chart clearly shows these relationships between students and items. Item fitness on the bubble chart and item discrimination on PUP Table 3a perform similar functions.

Next      Back     Start

Guttman Scalogram

Next   Back   Start                     Chapter 5

The information in Ministep Table 22.1 Guttman Scalogram of Responses has been re-plotted, to the right, into a perfect Guttman pattern. A string of right marks is followed by a string of wrong marks. In this perfect pattern, when a student misses a question on the test, all questions that are more difficult are also missed. The easiest question the student misses sets the student's ability. 

[Winsteps Table 22.2 Guttman Scalogram of Zoned Responses adds more information to PUP Table 3. 

Observations more than 0.5 rating points away from their expected category are marked with a letter equivalent: @ = 0, in expected category, and A = 1, just outside of expected category. 

The observations that are outside of their expected category are plotted in blue in this not so perfect world. Each blue mark shows a right answer assumed to be too difficult for that student. Green is both an unexpected and a too difficult right response. Only Item 20 shows a perfect performance pattern.

Otherwise there is a mix of right and wrong marks at the boundary of a student knowing and not knowing, and of a question being marked right or wrong, on PUP Table 3. Table 22.3 Guttman Scalogram of Original Responses is identical, in content, to PUP Table 3. PUP Table 3 is a Guttman Scalogram. 

Next     Back    Start

Item Discrimination

Next   Back   Start          Chapter 4

PUP Table 3 is re-tabled using three levels of item discrimination as PUP Table 3a. Mastery/Easy items survey student knowledge and provide a positive adjustment to the test score. Discriminating items divide the class into groups of students who know and who do not know. A change in instruction or special attention may be needed. Unfinished items reflect a problem in instruction, learning and/or testing.

Three easy items show how item discrimination works. Item 14 shows negative discrimination (ND) as only one high scoring student missed it. Item 11 shows positive discrimination (B) as only one low scoring student missed it. Item 20 shows the maximum positive value (A) as only the bottom two students missed it. This is an example of perfect item performance, a  Guttman pattern: a string of all correct marks followed by all wrong marks.

Although discrimination is not a part (a parameter) of the Rasch model, it is such an important descriptive statistic in managing the Rasch model that it is printed, in several forms, in both the person and the item statistics. Ministep therefore prints discrimination values rather then levels (A, B, C, and D) as printed by PUP. PUP and Winsteps calculate the same corrected point biserial r (pbr) when the “PTBISERIAL = Yes” control variable is used. PUP only prints the descriptive item or question pbr statistic.

These differences reflect the different optimization in the software. Winsteps maximizes the production of stable efficient tests. PUP optimizes easy to use data for instruction, testing and student counseling.

Items that tend to fit the Rasch model best also tend to be discriminating. Items 5, 6, 7, and 8, with a range of difficulty from 71% to 88% (average difficulty = 84%), will be used as common items to link two tests.

Next    Back   Start

All Most Unexpected Responses

Next   Back   Start          Chapter 3

Ministep prints out two identical Tables, 6.6 and 10.6, showing additional, less unexpected, responses to those in Table 6.5, persons, and Table 10.5, items. These less most unexpected wrong responses have been added in yellow to PUP Table 3 Student Counseling Mark Matrix with Scores and Item Difficulties.

Also four unexpected right answers are added in green. They raise the question, “How did these low scoring students manage to make right marks on these two difficult items?”  Was it luck, guessing, copying or an accurate report of knowledge? This question cannot be answered with the combined evidence from Winsteps posted on PUP Table 3.

Student marks that fit the Rasch model the best reside along a line separating yellow and uncolored wrong marks.  Red and green marks contribute the most to unfitness in the model. This makes good sense.

High scoring students are assumed to be careless in making wrong marks (red). Less able students are expected to be careless too (yellow). Low scoring students are suspect when making right marks on difficult questions (green). These are basic expectations of IRT.

PUP includes a guessing monitor (a quality score for judgment, only with Knowledge and Judgment Scoring^TM) and a copy detector (Sheets 8 and 9).

Next   Back   Start

Winsteps Item Most Unexpected Responses

Next   Back   Start                Chapter 2

A companion table to person most unexpected responses (Table 6.5) drawn from Winsteps Table 17.1 Person Statistics is the table of item most unexpected responses drawn from Table 13.1 Item Statistics.

The data from three columns in Table 13.1 are re-tabled into Winsteps Table 10.5 Most Unexpected Responses.

 These values are plotted, in red, on PUP Table 3. 

Item 11, with an estimated IRT difficulty measure of -1.51, is the easiest question any student missed, by Murta. Item 2, with an estimated IRT difficulty measure of 1.14, is the most difficult question with an unexpected response, by Martin. This rank of unexpected responses is again directly related to item difficulty on PUP Table 3. This makes good sense.

Difficult questions are expected to receive wrong marks. No wrong marks are expected on easy questions. High ability students are expected to mark difficult items correctly. These are basic expectations for IRT.

Of interest here is that the locations of the most unexpected responses for person and for item are identical on PUP Table 3. The person scan of PUP Table 3 is from highest score to lowest score, vertically, and the item scan of the table is from easiest to most difficult, horizontally.

These most unexpected responses are calculated on average and in general, as is characteristic of right mark scoring (RMS). The test instructions are to mark the best answer on every question. Students are not given the responsibility, and a reward, for reporting, on each specific question, what they know and do not know, as is done with Knowledge and Judgment Scoring^TM (KJS).

Next   Back   Start

Winsteps Person Most Unexpected Responses

Next  Back  Start            Chapter 1

The Rasch model IRT test score analysis has become a “commonly used statistical procedure” wrapped in layers of mystery. By contrast, right mark (or count) scoring (RMS) analysis is traditionally evaluated by just looking directly at a table of marks bounded by student test scores and question difficulty values.

One way to audit the Rasch model is to compare IRT and RMS analysis printouts. Many show identical data. Other IRT printouts provide valuable insights not present in RMS analysis.

A test of 24 students by 24 questions  was scored with Ministep and with Power Up Plus (PUP). Passing was 75% on this nursing school test.

Winsteps prints out identical data in Table 17.1 Person Statistics. Student names  are even listed in the same order for students with the same score.

The data from four columns in Winsteps Table 17.1 are re-tabled into Winsteps Table 6.5 Most Unexpected Responses.

 These values are plotted in red on PUP Table 3.


Hall, with an estimated IRT ability measure of 3.44 is the highest scoring student to have missed a question, #21. Murta, with an estimated IRT ability measure of 0.58, is the next to the lowest scoring student, missing #11, and seven more. This ranking of unexpected responses is directly related to student test scores. This makes good sense.

Top students are not expected to make wrong marks. No student is expected to miss easy questions. These are basic expectations for IRT.

Next  Back  Start