Rasch Model Student Ability and CTT Quality

                                                              47

How the Rasch model IRT latent student ability value is related to the classical test theory (CTT) PUP quality score (% Right) has not been fully examined. The following discussion reviews the black box results from Fall8850a.txt (50 students and 47 items with no extreme items) and then examines the final audit sheets from normal and transformed analyses. It ends with a comparison of the distributions of latent student ability and CTT quality. The objective is to follow individual students and items through the process of Rasch model IRT analysis. There is no problem with the average values.

We need to know not only what happened but how it happened to fully understand; to obtain one or more meaningful and usefully views. Fifty students were asked to report what they trusted using multiple-choice questions. They were scored zero for wrong (poor judgment), one point for omit (good judgment not to guess and mark a wrong answer), and two points for good judgment (to accurately report what they trusted) and a right answer. Knowledge and Judgment Scoring (KJS) shifts the responsibility for knowing from the teacher to the student. It promotes independent scholarship rather than the traditional dependency promoted by scoring a test only for  right marks and the teacher then telling students which marks were right marks (there is no way to know what students really trust when “DUMB” test scores fall below 90%).

Winsteps displays student and item performance in dramatic bubble charts. The Person & Item chart shows students in blue and items in red. Transposed results (columns and rows become rows and columns) are shown in an Item & Person chart where students are red and items are blue (basically everything has been turned upside down or end over end except the paint job). Blue student 21 with the highest measure (ability) lands as red student 21 with nearly the lowest measure when transposed. That is what is done. Why it is done comes later.

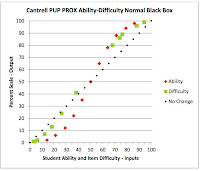
A plot of input/output logit values shows how the process of convergence changes the locations of latent student abilities (log right/wrong ratio of raw student scores) and item difficulties (log wrong/right ratio of raw item difficulties) so they end up as the values plotted on the bubble charts. The ranges of measures on the input/output charts are the same as on the bubble charts. The end over end tipping, from transposing, on the bubble charts also occurs on the input/output charts. Student abilities are grouped as items are treated individually (items with the same test score land at different points on the logit scale). When transposed, items difficulties are grouped as students are treated individually (students with the same test score land at different points on the logit scale). And, in either case, the distribution being examined individually has its mean moved to register at the zero logit location.

The end over end tipping, from transposition, also shows in the normal black box charts. It is easy to see here that the distribution being held as a reference shows little change during the process of convergence. The distribution being examined individually is widely dispersed. Only the highest and lowest individual values for the same grouped value are shown for clarity. Also a contour plot line has been added, for clarity, to show how the individual values would relate to the grouped values if a location correction were made for the fact that all of these individual values have been reduced by the distance their mean was moved to put it on the zero logit location during the process of convergence. In general, the individual values are disbursed about the contour line. This makes sense as they must add up to their original logit mean in the above input/output charts.

The above charts display the values on the final audit sheets for Fall8850a data. Values from Winsteps Table 17.1 Person Statistics were entered in column four Student Logit (+) Output. Values from Table 13.1 Item Statistics were entered in column ten, Item Logit (-) Output. Logit input values were derived from the log right/wrong and log wrong/right ratios for students and items. Normal input values are scores expressed as a percent. Normal output values are from the perfect Rasch model algorithm: exp(logit (+) output)/(1 + exp(logit (+) output)). Normal output (+) item values come from subtracting Normal (-) values from 100% (this inverts the normal scale order in the same way as multiplying values on the logit scale with a -1). One result of this tabling is that comparable output student ability and item difficult values that are clustered together add up to 100% (colored on the chart for clarity). This makes sense. A student ability of 79% should align with an item difficulty with 21% (both with a location of 1.32 logits).

The same thing happens when the data are transposed except, as noted in the above charts, everything is end over end. Column four is now Item Logit (+) Output from Winstep Table 17.1 Item Statistics and column ten, Student (-) Output, is from Table 13.1 Person Statistics. Again an item difficulty of 59% aligns with a student ability of 41% (both with a location of 0.37 logits).

Only normal values can be used to compare IRT results with CTT results. Sorting the above charts by logit input values from individual analyses (right side of each chart) puts the results in order to compare IRT and CTT results. Items 4, 34, and 36 had the same IRT and CTT input difficulties (73%). They had different IRT output values and different CTT quality (% Right) values. The item difficulty quality indicators change in a comparable fashion. (Normally a quality indicator (% Right) is not calculated for CTT item difficulty. It is included here to show how both distributions are treated by CTT and IRT analyses.)

CTT and IRT Quality Indicators
Method	Item (73% Input)
	34	4	36
CTT	83%	85%	93%
IRT	44%	46%	56%

Sorting the transposed analysis by input values groups student abilities. Four students had the same IRT and CTT abilities (70%). They had different IRT output values and CTT quality (% Right) indicators. The point is that these quality indicators behaved the same for student ability and item difficulty and for normal and transposed analyses. 

CTT and IRT Quality Indicators
Method	Student (70% Input)
	26	37	40	44
CTT	81%	88%	88%	95%
IRT	43%	51%	51%	63%
IRT + Mean	68%	76%	76%	88%

These quality indicators cannot be expected to be the same as they include different components. CTT divides the number of right answers by the total number of marks a student makes to measure quality (% Right). The number of right marks is an indicator of quantity. The test score is a combination of quantity and quality (PUP uses a 50:50 ratio). Winsteps combines IRT student ability and item difficulty, with the Rasch model algorithm, during the JMLE analysis into one expected value, at the same time, it is reducing the output value by the distance the mean location must be moved to the zero location point: convergence. CTT only sees mark counts. The perfect Rasch model sees student ability and item difficulty as probabilities ranging from zero to 1. A more able student has a higher probability of marking right than a less able student. A more difficulty item has a lower probability of being marked right than a less difficult item. This makes sense. A question ranks higher if marked right by more able students. A student ranks higher marking difficult items than marking easier items.

The chart of student ability, from normal and transposed analyses, plots the values for the students in the above table scoring 70% on the test. By following up from 70% Input you encounter 43, 51, and 63% transposed individual values below 76% for the grouped non-transposed value. 

The above selection of students and items was made from a PUP Table 3c. Guttman Mark Matrix. The two selections represented uneventful sets of test performances that seemed to offer the best chance for comparing IRT and CTT. PUP imports the unexpected values from Winsteps Tables 6.5 and 6.6 to color the chart. Coloring clearly shows the behavior of three students who never made the transition from guessing at answers to reporting what they trusted: Order 016, Order 031, and Order 035 with poor judgment scores (wrong) of 24, 13, and 26.

In conclusion, Winsteps does exactly what it is advertised to do. It provides the tools needed for experienced operators to calibrate items for standardized tests and to equate tests. No pixy dust is needed. In contrast, PUP with Knowledge and Judgment Scoring produces classroom friendly tables any student or teacher can use directly in counseling and in improving instruction and assessment. Winsteps with the Rasch partial credit model can perform the same scoring as is done with Knowledge and Judgment Scoring. The coloring of PUP tables provided by Winsteps adds more detail and makes them even easier to use.

There is no excuse for standardized tests and classroom tests being scored at the lowest levels of thinking. The crime is if you test at the lowest levels of thinking you promote classroom instruction at the same level (please see post on multiple-choice reborn). This holds for essay, report, and project assessment, as well as, for multiple-choice tests. The Winsteps Rasch partial credit model and PUP Knowledge and Judgment Scoring offer students a way out of the current academic trap: learning meaningless stuff for “the test” rather than making meaningful sense of each assignment that then empowers the self-correcting learner to learn more. The real end goal of education is developing competent self-educating learners. It is not to process meaningless information that is forgotten with each “mind dump” examination.

Personal computers have been readily available now for more than 30 years. Some day we will look back and wonder why it took so long for multiple-choice to be scored, as it originally was before academia adopted it; in such a manner that the examinee was free to accurately report rather than to continue an academic lottery used to make meaningless rankings.

Rasch Model Convergence Normal Black Box

                                                             46

The normal black box displays IRT results on a normal scale that can be compared directly to CTT values. The four charts from Fall8850a.txt, rating scale, culled rating scale, partial credit, and culled partial credit at not too different from the logit black box charts in the prior post. The un-culled data set included 50 students and 47 items. The culled data set included 43 students and 40 items (7 less outlying students and items each).

The first three charts show student abilities passing through the 50%, zero logit, point. Failure for this to be the case with culled partial credit was observed in the prior logit black box post, but is very evident in this normal scale chart. The culled partial credit analysis passed through three iterations of PROX rather than two for the other three analyses.

A curious thing was discovered when developing the extended normal values for student abilities. Up to now all extended student ability estimates only involved multiplying the log ratio value of student raw scores by an expansion factor. For the culled partial credit analysis, a shift value had to be included, as is normally done when estimating item difficulty values. A shift value was not needed when estimating student ability values with the un-culled partial credit data set, or any other data set I have examined. The plot of the extended student abilities would not drift away from the no change line without the additional shift of 0.4 logits.

Student scores are used as a standard in non-transposed analyses. The un-culled data set, using partial credit analysis, will now be used in a transposed analysis where item difficulties become the standard for the analysis. This may clarify the relationship between the quality and quantity scores from Knowledge and Judgment Scoring for each student and the single latent student ability value from Rasch IRT.

Rasch Model Convergence Logit Black Box

                                                             45

This view of Fall8850a.txt Winsteps results has been visited before. The difference is that now I have an idea of what the charts are showing in three ways:

1. The plot of student abilities for the rating scale analysis passes directly through the zero logit location indicating a good convergence. 2. The plots for student abilities and item difficulties are perfectly straight lines (considering my rounding errors), which again shows a good convergence. 3. The two lines are parallel, another indicator of a good convergence.

Culling increased the distribution spread to higher values for both analyses, as shown in the previous post. The plot of student abilities for culled partial credit did not pass through the zero logit location. Removing 7 students and 7 items has resulted in a poor convergence.

The item difficulty plots for the partial credit analysis are very different from those from the rating scale analysis. Here items starting convergence with the same difficulty can end up at various ending locations. The lowest and the highest locations are plotted for each item.

This post must end, as a comparison of Rasch IRT and PUP CTT results cannot be made directly between logit and normal scale values. 

Rasch Model Logit Locations

                                                              44

Student ability and item difficulty logit locations remain relatively stable during convergence when using data that are a good fit to the requirements of the perfect Rasch IRT model. The data in the Fall8850a.txt file requires that the average logit item difficulty value be moved one logit, from -.98 to 0, during convergence. The standard deviations for student ability and item difficulty, 0.51 and 1.0, are also quit different.

The relative location of individual student abilities and Item difficulties vary, from the two factors above and from the culling of data that “do not look right”, during the process of convergence on the logit scale. Individual changes in the relative location of student ability and item difficulty can be viewed by re-plotting the bubble chart data shown in the previous post.

The rating scale analysis groups all students with the same score and all items with the same difficulty. The end result is a set of nearly parallel lines connecting the starting and ending convergence location of a student or an item. (Closely spaced locations have been omitted for clarity.)

Culling outliers resulted in the loss of values among the less able students and the more difficult items.

This increased the student ability mean and decreased the item difficulty mean. Culling increased the spread of both distributions toward higher values.

The partial credit analysis groups all students with the same score but treats item difficulty individually. (More locations have been omitted for clarity.) Four of the plotted starting item difficulty locations land at more than one ending convergence location. Culling partial credit outliers had the same effects as culling rating scale outliers (above) related to where the culling occurred, the migration of means, and the direction of distribution spread. (More item difficulty locations were omitted for clarity.)

The item difficulty mean migrated to the zero logit, 50% normal, location in all four analyses: full rating scale, culled rating scale, full partial credit, and culled partial credit. Winsteps performed as advertised for psychometricians .

The individual relative locations for student ability and item difficulty differ in all four analyses. Two items, that survived my culling and omitting, have the same starting location but very different ending locations: Item 13 and Item 41. Both are well within the -2 to +2 logit location on the Winsteps bubble charts (item response theory – IRT data).

PUP lists them as the two most difficult items on the test (classical test theory – CTT data). PUP lists Item 13 as unfinished, with 15 out of 50 students marking, of whom only 5 marked correctly. There is a serious problem here in instruction, learning, and/or the item itself. Item 41 was ranked as negatively discriminating (four of the more able students in the class marked incorrectly). Only 5 students marked item 41 and none were correct. The class was well aware that it did not know how to deal with this item. Both items were labeled as guessing.

IRT and CTT present two different views of student and item performance. The classroom friendly CTT charts produced by PUP require no interpretation for students and teachers to use directly in class and when advising.

Culling Rasch Model Data

                                                             43

The past posts have been concerned with how IRT analysis works when using different ways to estimate latent student ability locations and item difficulty locations. So far it seems that with good data a student ability location and an item difficulty location, at the same point on the logit scale, do represent comparable values. They will never make a perfect fit as that can only happen if the student ability and item difficulty distributions have means of 50% or zero logits and they have the same standard deviation or spread.

The perfect Rasch IRT model can never be completely satisfied. Winsteps, therefore, contains several features to remove data that “do not look right”. For this post, students and items more than two logits away from the bubble chart means were removed (that is more than about two standard deviations). The Fall8850a.txt file with 50 students and 47 items (no extreme values) was culled by 7 students and 7 items to 43 students and 40 items.

In both cases, rating scale and partial credit, culling resulted in lowering the standard error of locations (smaller bubbles). This improved the analysis. In both cases it also increased the estimated latent student ability and item difficulty locations. Getting rid of outliers, made the overall performance on the test look better.

Rasch Model Student Ability and Item Difficulty

                                                              42

Do equivalent individual latent student ability and item difficulty calibration locations really match? They do at the zero logit or 50% normal location. A successful convergence places the two distribution means at this same location.

The Cantrell logit PUP PROX data (see prior post) show the student ability and item difficulty locations successfully centered on or near the zero logit location. The average test score is 48%. Also the locations are successfully plotted in perfectly straight lines on the logit scale. However, the ability and difficulty distributions do not have the same rates of expansion and they are not parallel.

The Cantrell normal PUP PROX conversion from the logit scale throws the student ability distribution into an S-shaped curve. It is still centered at the 50% point.

When the latent student ability locations are being expanded on the logit scale during convergence, they are moving at logit speed (2.718 times faster than normal speed). The farther they are away from zero, the faster they move. The result is a grouping of locations in the outer arms of the normal distribution.

The Cantrell Winsteps data show even greater dispersion after ten JMLE iterations past the PUP PROX data. The zero location is not maintained, and S-shaped curves have now developed in both ability and difficulty distributions. These become even more exaggerated when converted to normal values.

This development of an S-shaped curve results from expanding student ability locations. A chart based on the Rasch model curve shows the effect of expansion from one (no change) to four times. PUP PROX yielded an expansion factor of 2.15 and Winsteps yielded an estimated 3.09. Convergence operations are carried out on a linear logit scale. When converted, the normal student ability results are thrown into an S-shaped curve where the locations clump at the ends of the distribution.

The Nursing1 logit, PUP PROX and Winsteps (PROX & JMLE), results show very different results from Cantrell results. The average test score is 80% rather than 48% (mastery rather than meaningless ranking). Student ability locations are successfully centered on the zero location. Both ability and difficulty distributions are plotted in perfectly straight lines. A difference in average raw score between the two data sets, of 32%, has moved the item difficulty location distribution far away from the zero location. The initial shift of the average input Nursing1 item difficulty logit location was 1.62 logits.

The Nursing1 normal PUP PROX conversion from the logit scale results in a large curve for item difficulty locations and a shallow S-shaped curve for student ability locations. The full nature of the curves was exposed by extending the data.

A linear shift of zero (no change) and 0.5, 1.0, and 1.5 logits of item difficulty locations shows how the curve in the Nursing1 data developed -- the greater the shift, the lower the curve. Item difficulty locations did not migrate toward the ends of their distribution as do student ability locations.

Both PUP non-iterative PROX and Winsteps, iterative PROX and JMLE, produce the desired results when fed good test score data. I can now understand the reason for the many features included in Winsteps to help skilled operators to detect and cull data that does not meet the requirements of the perfect Rasch model.

The Cantrell data do not fit the requirements. This may be part of the reason Cantrell failed to find student ability and item difficulty independence. 

Good data must then have similar distributions (standard deviations). The average test score does not need be near 50% for a good convergence.

I am calling the Nursing1 data a good fit for dichotomous Rasch model analysis based on three observations: 1. Both PUP PROX and Winsteps obtained the same analysis results (non-iterative PROX and iterative PROX:JMLE). 2. The relative location of student ability and item difficulty remained stable from input to output. 3. The logit plot is a perfectly straight line for both student ability and item difficulty locations (considering rounding errors).

Dichotomous Rasch Model Audit

                                                             41

The internal black box audit tool, introduced in the previous post, provides a clear view of what is happening on the logit scale during convergence. Three sets of answer sheets provide the needed data to explore these happenings with average test scores of 80%, 59%, and 48%. These three values as associated with mastery, passing in the classroom, and optimum for psychometric analysis.

Student and Item Data
	Score	Initial Standard Deviation	Number
Nursing1	80:20	0.70:0.95	22:21
EDS - Moulton	59:41	0.97:1.63	9:10
Cantrell	48:52	0.85:2.20	34:14

The Nursing1 chart shows the input values evenly spaced with the exception of a very small ever-expanding distribution. This “error” is an artifact of converting normal values to logit values. The input item difficulty values are shifted to comparable student ability values in an orderly manner, that is, the lines are parallel. The average item difficulty logit value is relocated to zero. This data set represents a good fit to the Rasch model, given my current understanding. The relative positions of student ability and item difficulty remain stable from input to output.

The EDS data shows student ability and item difficulty expanding at two different rates. Here the initial standard deviations differ more than in the Nursing1 data. The result is that the relative positions of student ability and item difficulty changed from input to output.

The Cantrell data are centered near the 50% normal or zero logit location. There was no need to relocate item difficulties, as was done with the Nursing1 data. There was a need to respond to the two very different initial standard deviations. This caused the student abilities to be expanded far faster than the item difficulties.

A second observation on the Cantrell data relates PUP non-iterative PROX and Winsteps results. Winsteps results at four JMLE iterations compared to PUP PROX results. Winsteps then continued ten more JMLE iterations before convergence was called. This both increased the expansion of the distributions but also increased the change in the relative locations of student ability and item difficulty from input to output.

The destabilizing factor seems to be the relative spread of the two distributions for student ability and item difficulty. Statistically the distributions (standard deviations) are being matched, when converging, for the Cantrell and EDS data, but the process changes the relative individual locations.

Good data must then have similar distributions (standard deviations). Also the values need to fall within about -2 to +2 logits (12% to 88% normal).

I am calling the Nursing1 data a good fit for dichotomous Rasch model analysis based on two observations: 1. Both PUP PROX and Winsteps obtained the same results (non-iterative PROX and iterative PROX:JMLE). 2. The relative location of student ability and item difficulty remained stable from input to output.

Rasch Model Convergence Black Box

                                                             40

When this audit started over two years ago, I never planned to travel inside the Rasch model algorithms. Surely by taking a close look from outside (the black box audit tool) one could satisfy that no pixy dust was needed to accomplish the proclaimed feats. The fact that several claims have been discounted in the past ten years, after being applied to NCLB standardized paper tests, makes me question the basic process of estimating item difficulty and student ability measures. (This doubting has nothing to do with the successful application of the Rasch model in many other areas.)

A number of things have raised my doubts. Normal test results cannot be given special value by converting from normal to logit values. The perfect Rasch model is a curve, not a straight line. Laddering across several grades is now in question (in part IMHO because the tests are still scored at the lowest levels of thinking – a guessing exercise -- rather than giving students the option to report what they actually trust – Knowledge and Judgment Scoring). Even some psychometricians still doubt the claims made for the Rasch model.

The black box audit tool that I have been using relates what goes on inside the full Rasch model to the normal world. Conversions of normal to logit and logit to normal add nothing to the audit tool. And nothing has been found amiss. A better audit tool is needed now that we are inside the full Rasch model.

The various ways of estimating student ability and item difficulty measures make use of the original student marks on the test, the student score, the item difficulty, and their distributions (mean and standard deviation). One end result from the transposed Rasch partial credit model is that the estimated individual latent student ability expresses, in one term, what is presented by Knowledge and Judgment Scoring in two terms: quantity and quality. Quantity and quality are directly related to student marks. Estimated latent student ability is dependent upon an estimate of how student marks are related to item difficulty: convergence.

This new black box audit tool relates just these internal values. The two EDS distributions, from the previous post, for student ability and item difficulty, radiate from different starting points and expand at different rates. The span from -2 to +2 logits covers the expected score range from 12% to 88%.

The relative locations for student abilities and item difficulties increasingly change from the positive to the negative regions of the logit scale. This maybe intended or is just an acceptable artifact to psychometricians. It presents a problem for state departments of education that claim their tests are so difficult that passing can be set around 40% on NCLB standardized tests. (I would think this region would be of very little interest in the classroom where the customary passing point is 60% and the average test score is 75%. It is of no interest when hidden by state departments of education by only reporting passing rates without reporting test scores.)

I read the individual student abilities and item difficulties plots, from the internal audit black box tool, to mean that item difficulty is being reported increasingly higher than the comparable student ability, the lower the item difficulty. This would make a test using these items easier than expected in this region, the region of super low cut scores.

Distribution statistics do not reveal individual student and item performances.  Instead they show that, as the item difficulty mean of -0.44 was relocated very near to zero, the student ability mean drifted from 0.39 to 0.71 log its.

The rate of expansion for student ability was larger than for item difficulty. This did little to match the two distributions. The expansion of the two logit distributions was very linear. Yet the end result of the analysis, in normal values, was S-shaped curves.

If the distribution statistics are acceptable, does it matter what happens to individual students? I think so. This is an example of why research techniques do not always work in the application environment.

The best defense students have is to actually know their subject or master the skill to the point that passing is assured. Trying to pass with one point over the line is as flawed a student method as is the state department of education method of setting the cut score before the test is scored to see what actually happened. Application has more serious individual requirements than research.

One auditing method that I have yet to see used is for teachers to include a ranking of their students with the answer sheets. An even better method IMHO is for students to rank themselves by electing Knowledge and Judgment Scoring and reporting what they trust (using all levels of thinking) rather than taking the traditional forced-choice test based on the lowest levels of thinking (meaningless guessing in the cut score region). [Meaningless to everyone except psychometricians only interested in ranking performance.]