Rasch Model Student Ability and Item Difficulty

                                                              42

Do equivalent individual latent student ability and item difficulty calibration locations really match? They do at the zero logit or 50% normal location. A successful convergence places the two distribution means at this same location.

The Cantrell logit PUP PROX data (see prior post) show the student ability and item difficulty locations successfully centered on or near the zero logit location. The average test score is 48%. Also the locations are successfully plotted in perfectly straight lines on the logit scale. However, the ability and difficulty distributions do not have the same rates of expansion and they are not parallel.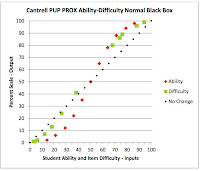

The Cantrell normal PUP PROX conversion from the logit scale throws the student ability distribution into an S-shaped curve. It is still centered at the 50% point.

When the latent student ability locations are being expanded on the logit scale during convergence, they are moving at logit speed (2.718 times faster than normal speed). The farther they are away from zero, the faster they move. The result is a grouping of locations in the outer arms of the normal distribution.

The Cantrell Winsteps data show even greater dispersion after ten JMLE iterations past the PUP PROX data. The zero location is not maintained, and S-shaped curves have now developed in both ability and difficulty distributions. These become even more exaggerated when converted to normal values.

This development of an S-shaped curve results from expanding student ability locations. A chart based on the Rasch model curve shows the effect of expansion from one (no change) to four times. PUP PROX yielded an expansion factor of 2.15 and Winsteps yielded an estimated 3.09. Convergence operations are carried out on a linear logit scale. When converted, the normal student ability results are thrown into an S-shaped curve where the locations clump at the ends of the distribution.

The Nursing1 logit, PUP PROX and Winsteps (PROX & JMLE), results show very different results from Cantrell results. The average test score is 80% rather than 48% (mastery rather than meaningless ranking). Student ability locations are successfully centered on the zero location. Both ability and difficulty distributions are plotted in perfectly straight lines. A difference in average raw score between the two data sets, of 32%, has moved the item difficulty location distribution far away from the zero location. The initial shift of the average input Nursing1 item difficulty logit location was 1.62 logits.

The Nursing1 normal PUP PROX conversion from the logit scale results in a large curve for item difficulty locations and a shallow S-shaped curve for student ability locations. The full nature of the curves was exposed by extending the data.

A linear shift of zero (no change) and 0.5, 1.0, and 1.5 logits of item difficulty locations shows how the curve in the Nursing1 data developed -- the greater the shift, the lower the curve. Item difficulty locations did not migrate toward the ends of their distribution as do student ability locations.

Both PUP non-iterative PROX and Winsteps, iterative PROX and JMLE, produce the desired results when fed good test score data. I can now understand the reason for the many features included in Winsteps to help skilled operators to detect and cull data that does not meet the requirements of the perfect Rasch model.

The Cantrell data do not fit the requirements. This may be part of the reason Cantrell failed to find student ability and item difficulty independence. 

Good data must then have similar distributions (standard deviations). The average test score does not need be near 50% for a good convergence.

I am calling the Nursing1 data a good fit for dichotomous Rasch model analysis based on three observations: 1. Both PUP PROX and Winsteps obtained the same analysis results (non-iterative PROX and iterative PROX:JMLE). 2. The relative location of student ability and item difficulty remained stable from input to output. 3. The logit plot is a perfectly straight line for both student ability and item difficulty locations (considering rounding errors).